在简书平台上,有一个热门话题吸引了小明的目光——“04.寻找两个有序数组的中位数(难度:困难)”。作为一名对算法充满热情的学习者,他决定迎接这个挑战。今天,就让我们跟随他的脚步,一起探索这个经典的算法问题。
什么是中位数?
中位数是一个统计学概念,指的是将一组数据从小到大排列后位于中间位置的数值。如果数据个数是奇数,那么中位数就是正中间的那个数;如果是偶数,则中位数为中间两个数的平均值。
对于这个问题,我们需要找到两个已经排序好的数组合并后的中位数。这看似简单,但要以高效的方式实现却并不容易。
初探解法
小明首先尝试了最直接的方法:将两个数组合并成一个数组,然后重新排序,最后根据长度计算中位数。这种方法虽然易于理解,但时间复杂度较高,为O((m+n)log(m+n)),其中m和n分别为两个数组的长度。显然这不是最优解。
接着,他开始思考如何利用两个数组已经排序的特点来优化算法。通过查阅资料,小明了解到一种基于二分查找的解决方案,这种方法可以将时间复杂度降低到O(log(min(m, n)))。
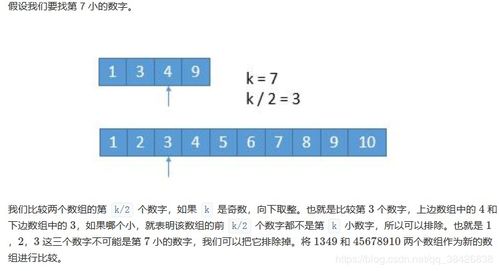
深入解析二分查找法
假设我们有两个数组A和B,长度分别为m和n。为了简化问题,我们可以假设m ≤ n。接下来,我们需要在较短的数组A中进行二分查找,找到一个分割点i,使得:
- A[i-1] ≤ B[j]
- B[j-1] ≤ A[i]
其中j = (m + n + 1) / 2 - i。这样,我们就能够确保左侧所有元素都不大于右侧所有元素。
根据分割点的位置,我们可以轻松地计算出中位数:
- 如果总长度为奇数,中位数为max(A[i-1], B[j-1])。
- 如果总长度为偶数,中位数为(max(A[i-1], B[j-1]) + min(A[i], B[j])) / 2。
实践与调试
小明按照上述思路编写了代码,并进行了多次测试。起初,他在处理边界条件时遇到了一些问题,例如当某个数组为空或者分割点位于数组两端时的情况。经过反复调试,他终于成功解决了这些问题。
最终,他提交了自己的代码,并通过了所有的测试用例。这次经历让他深刻体会到算法学习的乐趣与挑战。
总结
通过解决“寻找两个有序数组的中位数”这一难题,小明不仅提升了自己对二分查找的理解,还学会了如何更高效地分析和解决问题。相信在未来的学习道路上,他会继续勇往直前,不断突破自我。




发表评论 取消回复