贝叶斯拒绝法：数据科学中的新宠，你真的了解它吗？

导读：

• 什么是贝叶斯拒绝法？
• 贝叶斯法则的历史背景
• 在现代数据分析中的应用
• 贝叶斯拒绝法的优势与挑战
• 未来展望与思考

什么是贝叶斯拒绝法？

贝叶斯拒绝法（Bayesian Rejection Method）是统计学中一种基于贝叶斯定理的推断方法。它主要用于在面对不确定性时，如何根据新的证据调整我们对某一假设的信任程度。

这种方法的核心在于“先验概率”和“后验概率”的概念。简单来说，先验概率是我们对某个事件发生概率的初步估计，而后验概率则是在获得新信息后更新的概率。

贝叶斯法则的历史背景

贝叶斯法则最早由18世纪英国数学家托马斯·贝叶斯提出，并在其去世后由朋友理查德·普赖斯整理发表。随后，皮埃尔-西蒙·拉普拉斯进一步推广了这一理论，使其成为现代统计学的重要基础之一。

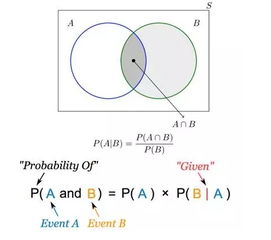
贝叶斯法则的基本形式如下：
$$ P(H|E) = \frac{P(E|H) \cdot P(H)}{P(E)} $$
其中，$ P(H|E) $ 是在观察到证据 $ E $ 后假设 $ H $ 成立的概率，即后验概率；$ P(E|H) $ 是在假设 $ H $ 成立的情况下观察到证据 $ E $ 的概率；$ P(H) $ 是假设 $ H $ 的先验概率；而 $ P(E) $ 是所有可能假设下观察到证据 $ E $ 的总概率。

在现代数据分析中的应用

随着大数据时代的到来，贝叶斯拒绝法在多个领域得到了广泛应用。例如，在机器学习中，贝叶斯优化方法被用来高效地搜索最优超参数组合。

这些方法可以分为三类：
(1) 匹配或重新加权方法，例如最佳子集、正则化权重以及面板匹配；
(2) 显式结果建模方法，例如贝叶斯结构时间序列模型、潜在因子模型(LFMs)以及矩阵补全方法；
(3) 双重稳健方法，例如增强型合成控制法和合成差异法(DiD)。

贝叶斯拒绝法的优势与挑战

贝叶斯拒绝法的最大优势在于其能够灵活地结合先验知识与新数据，从而提供更为精确的预测和决策支持。然而，这种方法也面临着一些挑战，如计算复杂度高、需要大量数据支持等。

"贝叶斯拒绝法并不是万能钥匙，但它确实为我们打开了一扇通往更准确预测的大门。" —— 某知名数据科学家

未来展望与思考

尽管现有方法尚未完全解决所有问题，但随着计算能力的提升和算法的不断改进，贝叶斯拒绝法在未来有望在更多领域发挥重要作用。

无论是金融风险评估、医疗诊断还是市场营销策略制定，贝叶斯拒绝法都将成为不可或缺的工具。